1. Nelijohtoisessa ryhmässä rekisteröitiin käynnissä olevien puheluiden lukumäärä 10 kiiretunnin aikana 1 minuutin välein. Tuloksena oli:

   

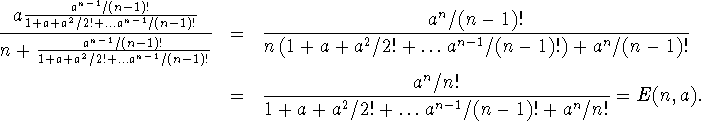
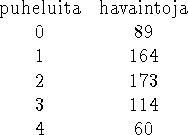
   Lisäksi estyneitä puheluita oli 34. Olettaen, että puhelut ovat mittausjaksojen aikana saapuneet Poisson-prosessin mukaisesti (kutsuesto ja aikaesto ovat yhtä suuret) vakiointensiteetillä, arvioi keskimääräinen puhelun kestoaika ja keskimääräinen tarjottu liikenneintensiteetti.

     
   Figure: Käynnissä olevat puhelut
   

   Havaintojen kokonaismäärä on 600. Todennäköisyys että kaikki johdot ovat varattuja on 60/600 = 0.1 (aikaesto). Nyt

   

   Edelleen välitetty liikenneintensiteetti = keskimäärin käynnissäolevien puheluiden lkm. eli

   

   Olkoon keskimääräinen puhelun kesto. Nyt

   

   josta .

   Nyt keskimääräinen tarjottu liikenne = .

2. Palvelukeskuksessa on 5 modeemia. Saapuvista soitoista 10% estyy sen vuoksi, että kaikki modeemit ovat varattuja. Mikä on tarjotun liikenteen intensiteetti (oletetaan poissonisiksi; uusintasoittoja ei huomioida)? Kuinka monta modeemia tarvitaan, jotta esto pienenisi 1 %:iin?

   Tasapainossa tilan j todennäköisyys 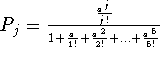missä . Aikaesto on tilan s=5 todennäköisyys:

   

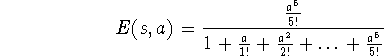
   Mikäli liikenteen tulointensiteetti on , on estyneiden puhelujen määrä systeemin tilassa 5 viettämä aikaosuus kertaa tulointensiteetti . Eli . Nyt . Likiarvo liikenteen intensiteetille saadaan esimerkiksi Mathematicalla tai likim. katsomalla käyrästöstä: .

   Tarvittavien modeemin määrä jotta estotodennäköisyys pienenisi 1%:iin saadaan esimerkiksi iteroimalla Mathematicalla:

   In[25]:= (a^6/6!)/Sum[ a^i/i!, {i,0,6}]
   Out[25]= 0.0458179
   In[26]:= (a^7/7!)/Sum[ a^i/i!, {i,0,7}]
   Out[26]= 0.0185088
   In[27]:= (a^8/8!)/Sum[ a^i/i!, {i,0,8}]
   Out[27]= 0.00662153

   Eli tarvitaan 8 modeemia.
3. Postimyyntiyhtiössä on tilaussoittoja vastaanottamassa 3 henkilöä. Puheluita saapuu Poisson-prosessina nopeudella 1/min ja puhelun keskipituus on 2 min.

   a) Millä todennäköisyydellä saapuva puhelu estyy, kun estyneitä puheluyrityksiä ei uusita?

   b) Kannattaako neljännen vastaajan palkkaaminen, jos vastaajan kokonaiskustannukset ovat 100 mk/h ja tuotto tilausta kohti on keskimäärin 20 mk?

   Kyseessä on Erlangin menetysjärjestelmä 3:lla tai 4:llä palvelijalla (M/M/K/K-systeemi, missä K = 3 tai 4).

   Tilausten intensiteetti (kuorma) .

   Koska kyseessä on Poisson-prosessi, kutsuesto ja aikaesto ovat samat.

   a)

   Lasketaan tilan kolme todennäköisyys (K=3) joko käsin tai katsomalla likiarvo käyrästöstä:

   

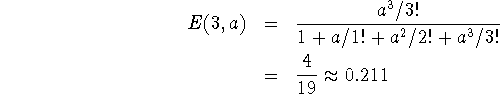
   b)

   Nyt K=4. Neljännestä henkilöstä on hyötyä kun palveltavana on 4 asiakasta. Lasketaan tilan neljä todennäköisyys:

   

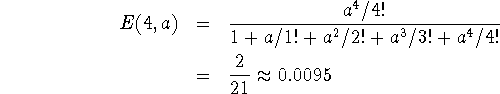
   Nyt estynyt liikenne pienenee (eli läpi mennyt kasvaa) määrällä . Joten nettomuutos on

   

   Ts. neljännen palvelijan palkkaaminen kannattaa.

4. Viiden johdon muodostamaan Erlangin menetysjärjestelmään saapuvan liikenteen intensiteetti on A=5 Erl. Estyneet kutsut tarjotaan kuljetettavaksi ylivuotojohdolla. a) Mikä on ylivuotoliikenteen intensiteetti? b) Mikä osuus ylivuotoliikenteestä estyy ylivuotojohdolla? Ohje: Alkuperäinen systeemi ja ylivuotojohto yhdessä muodostavat kuuden johdon järjestelmän. c) Mikä olisi ylivuotojohdon esto, jos sille tarjottu ylivuotoliikenne olisi Poissonista, jolloin tarjotusta liikenteestä estyisi Erlangin kaavan mukainen osuus.

   

   a)

   

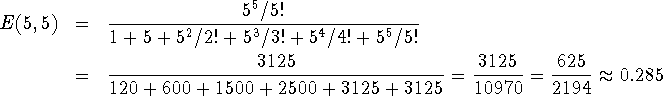
   Joten ylivuotoliikenteen intensiteetti on

   

   b)

   Esto mikäli systeemissä olisi 6 johtoa on

   

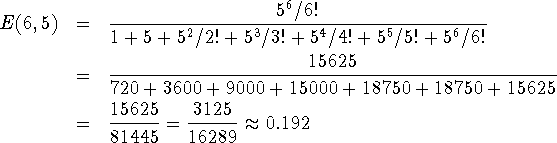
   Eli tulevista pyynnöistä ei mahdu edes ylivuotojohdolle. Nyt kysytty osuus on

   

   c)

   Mikäli ylivuotojohdolle tarjottu liikenne olisi Poissonista intensiteetillä saadaan estoksi

   

   Ero johtuu siitä että ylivuotojohdolle tuleva liikenne on purskeisempaa ja täten kutsuneston todennäköisyys on myös suurempi.

5. Näytä, että Erlangin funktio E(n,A) toteuttaa rekursiokaavan

   

   Sijoitetaan E(n-1,a) yhtälön vasemmalle puolelle:

   

• About this document ...