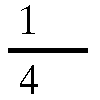 p / oikea merkintä paitsi M/M/1
p / oikea merkintä paitsi M/M/1
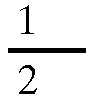 p)
p)Teletekniikan laboratorio
5. a) Selvitä yhdellä lauseella edellä annetussa kaavakokoelmassa olevat seuraavat
merkinnät:
M/M/1 =
q =
N =
s =
[[sigma]]s =
[[rho]] =
tq = (2 p.)
b) Oletaan viisi 9600 bps linkkiä, jotka kytkevät kaksi LANia toisiinsa. Pakettikoko linkeissä on 100 oktettia. Palveluajan keskihajonnaksi on saatu 0.079. Huippukuormituksen aikana paketteja saapuu 48 kpl/s. Saapuvat paketit ovat tasaisesti jakautuneet linkeille.
Voidaanko näiden tietojen perusteella laskea kunkin linkin huippukuormitus?
Jos mielestäsi
EI voida -> kerro miksi ei
KYLLÄ voidaan -> laske mikä on kunkin linkin huippukuormitus ja paketin
keskimääräinen jonotusaika sekä kerro mitä mallia (em.
kaavakokoelman (a),(b) vai (c) mallia) ja miksi käytit hyväksi? (4 p.)
==============================================================
==============================================================
RATKAISU
5.
Ratkaisut löytyvät Byte-lehden artikkelista prujuista.
a) (
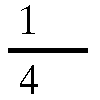 p / oikea merkintä paitsi M/M/1
p / oikea merkintä paitsi M/M/1
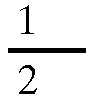 p)
p)
M/M/1 = kutsut saapuvat Poisson-prosessin mukaisesti / palveluajat eksponentiaalisesti
jakautuneita / palvelupaikkojen lukumäärä on 1 (ja odotuspaikkojen määrä on )
q = asiakkaitten lkm systeemissä (palveltavina ja jonossa)
N = palvelupaikkojen lkm
s = palveluaika
[[sigma]]s = palveluajan hajonta
[[rho]] = kuormitus
tq = tw + s = keskiarvoaika jonka asiakas viettää systeemissä (jono+palvelu)
b) KYLLÄ voidaan
paketti = 100 oktettia = 100 * 8 bit = 800 bit
Yhden paketin palveluaika s = = 0.0833 s (1 p)
Paketit tasaisesti jakautuneet linkeille [[??]] kullekin linkille huippu [[lambda]] = 48/5 = 9.6 pak/s
Siten huippukuormitus [[rho]] = [[lambda]]*s = 9.6 * 0.0833 = 0.8 (1 p)
Paketin palveluajan hajonta (0.079 s) on suunnilleen sama kuin palveluaika (0.0833 s)
[[??]] eksponentiaalinen palveluaikajakauma
[[??]] kaavakokoelman b-malli (M/M/1) (1 p)
[[??]] jonotusaika tw = = = 0.33 s (1 p)
(hyväksytty myös syst.vietetyn ajan lasku tq = = 0.42 s )