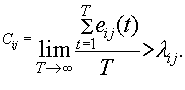 (1)
(1)I Polkukytkentä – Puolistaattinen reitityskaavio
suurimittaisille ATM pakettikytkimille
Closin verkkoa on käytetty mallina monille suuren mittakaavan ATM kytkinarkkitehtuureille, joissa hankalin vaihe on suorittaa polun ja kaistanleveyden määritys jokaiselle yhdistämispyynnölle. Staattinen reititystapa ei kunnolla käytä hyväksi staattista kanavointia. Toisaalta dynaaminen reititysmenetelmä vaatii reitityksen suorittamista jokaiselle korttipaikalle erikseen. Polkukytkentä on kompromissi näiden kahden reititysmenetelmän välillä. Se käyttää keskivaiheessa ennaltamääriteltyä periodista kytkentämallia, "katso ylös" valintaa otto vaiheessa sekä antojonotusta viimeisessä vaiheessa. Polkukytkennän skedulointi muodostuu kapasiteettin määrittämisestä ja reititin määrittämisestä. Kytkentäpyyntöjen palvelun laatu asettaa rajat kapasiteetti määrittämiselle. Reititys perustuu aikavälien lomitukselle, missä on käytetty kaksipuolisia multigraafeja.
Laajakaistadigitaaliverkkojen haaste on tukea virtuaalipiirikytkentöjä niin että ne voivat tarjota multimedia palveluita. Tähän ATM on tuonut varteenotettavan ratkaisunsa, mikä perustuu pitkälti ATM kytkinten kykyyn hallita erisuuria kaistanleveyksiä sekä erilaisia "palvelun laatu" tasoja. Solukytkentä perustuu niin sanottuun datagrammien reititykseen ns. "kytkentätehtaissa". Ristiriidat verkkotyöskentelyn ja kytkennän välillä voivat johtaa ristiriitaisiin verkkokerroksen protokolliin. Vältääkseen tämän ollaan nyt ehdottamassa puolistaattista reitityskaaviota nimeltä polkukytkentä.
Monet viimeaikoina ehdotetuista ATM-kytkin arkkitehtuureista perustuvat modulaariseen Clos-arkkitehtuuriin. Mallin isänä on mies nimeltä Charles Clos ja se oli tarkoitettu piirikytkentäisille järjestelmille. Siinä yhteys on erikseen järjestetty koko yhteysajalle kun taas ATM pakettikytkimet kuljettavat informaatiota kanavoidussa muodossa.
Polkukytkennässä yhdistyvät siis staattinen sekä dynaaminen reititysmenetelmä eli se perustuu ns. virtuaalisiin polkuihin Closin verkossa. Skeduloinnissa on siis kaksi osaa, joista ensimmäisessä liikenne arvot märäävät vaadittavan kapasiteetin jokaiselle virtuaaliselle polulle. Näin saavutetaan riittävä palvelutaso.Toiseksi kapasiteettin määrittävän matriisin mukaan määräytyy lopullinen kaksipuolisten multigraafien määrä. Jos kytkintä operoidaan näin jatkuvasti tällaisten yhteyskuvioiden mukaan, voidaan jokaisen virtuaalipolun kapasiteettivaatimukset saada riittävän hyviksi pitkällä aikavälillä.
II Polkukytkennän perusteet
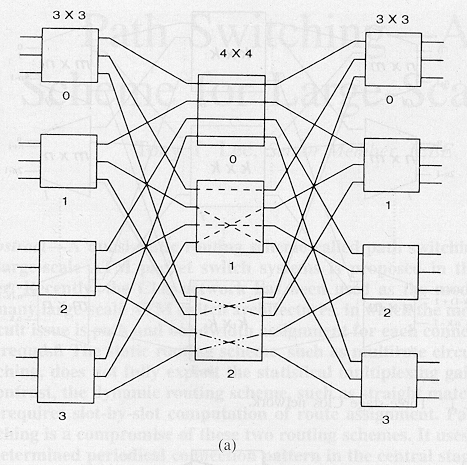
Kolmiportainen Closin verkko on esitetty kuvassa 1. Ensimmäinen porras sisältää k sisääntulomodulia, joista jokainen on n x m -kokoinen. Keskimmäisessä portaassa on k x k -kytkintä. Reititys verkossa tapahtuu seuraavien periaatteiden mukaan:
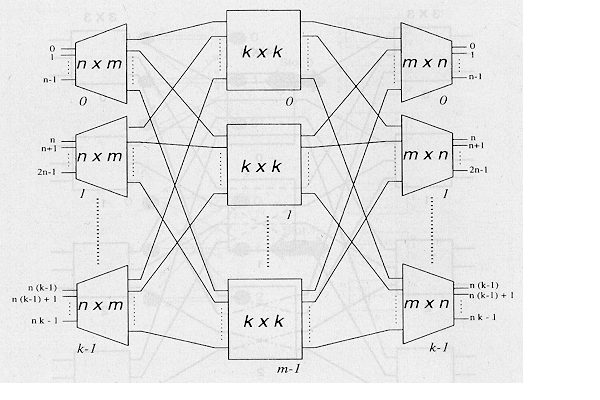
Kuva 1. Kolmiportainen Closin verkko.
Tulo- ja lähtömodulit ovat solmuja. Tietty kytkentäjärjestys keskimmäisessä portaassa voidaan esittää säännöllisinä kaksipuoleisina kytkentöinä m-asteisissa solmuissa (kuva 2). Jokainen keskimoduli vastaa n-särmäistä ryhmää. Särmistä kukin kytkee yhden parin tulo- ja lähtömoduuleita. Jos reititysalgoritmi perustuu dynaamiseen solujen kytkentään ja liikenteen määrä tulomodulista Ii lähtömoduliin Oj on l ij solua aikaväliä kohti, niin kytkentäjärjestys muuttuu joka aikavälissä tulopakettien mukaan. Tässä tapauksessa reititys lasketaan joka aikavälille erikseen. eij(t) on särmien lukumäärä Ii:stä Oj:hin kaksipuoleisessa graafissa aikaväliä t kohti. Virtuaalipolun kapasiteetin Cij täytyy Ii: ja Oj:n välillä täyttää ehto
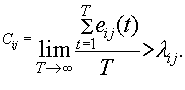 (1)
(1)
Toisaalta piirikytkentäisen Closin verkon reititys on kiinteä ja kytkentäjärjestys on pysyvä joka aikavälissä. Kapasiteetin täytyy olla
![]() (2)
(2)
joka merkitsee sitä, että Cij on virtuaalipiirin maksimikaistanleveys puhelun kytkennän aikana. Täten ei hyödynnetä ollenkaan tilastollista multipleksausta. Tähän ongelmaan on esitetty ratkaisuksi puolistaattista reititystä, polkukytkentää, jossa käytetään äärellistä märää erilaisia kytkentäjärjestyksiä keskiportaassa. Tämä on kompromissi edellä esitetyille kahdelle reititystavalle. Jokaiselle annetulle l ij, jos å il ij < n £ m, voidaan määritellä äärellinen määrä f kaksipuoleisia graafeja siten, että
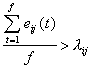 (3)
(3)
missä eij(t) on särmien lukumäärä solmusta i solmuun j t:nnessä graafissa. Kapasiteettivaatimus (1) voidaan saavuttaa, jos järjestelmä kykenee tekemään jatkuvasti kytkentöjä, jotka vastaavat näiden graafien polkuja ja tämä reititystieto voidaan tallentaa jokaisen modulin muistiin, jotta jokaiselle
aikavälille ei tarvitse laskea reititystä. Polkukytkentä vastaa piirikytkentää kun f=1, ja solukytkentää kun f à 8.
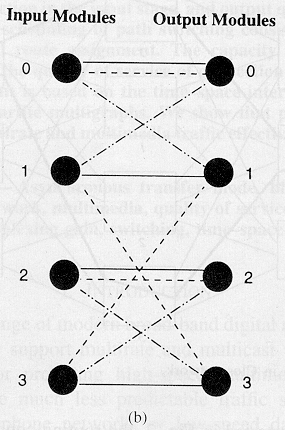
Kuva 2. Closin verkon keskiportaan reitityksen ja kaksiportaisen graafin särmien vastaavuus. (a) Closin verkko.
(b) Kaksipuoleinen graafi.
Polkukytkennän määrittäminen koostuu kahdesta vaiheesta, kapasiteetin ja reitin määrityksestä. Kapasiteetin määrittäminen tarkoittaa jokaisen virtuaalipolun kapasiteetin Cij>l ij laskemisesta tulomodulin Ii ja lähtömodulin Oj välillä. Se voidaan tehdä optimoimalla jotain funktiota å iCij = å jCij = m suhteen. Funktion valinta riippuu virtuaalipolun liikenteen stokastisista ominaisuuksista ja kytkentöjen laatuvaatimuksista.
Seuraava vaihe on muuntaa kapasiteettimatriisi [ Cij] äärelliseksi määräksi f särmien graafeja, joista jokainen vastaa tiettyä kytkentäjärjestystä Closin verkon keskiportaassa. Tarkoituksena on laskea m erilaista polkua m:ään eri särmään joka solmussa siten, ettei missään kahdessa vierekkäisessä särmässä ole samaa polkua. Jokainen polku vastaa keskimodulia, ja polun määritys tulomodulista i lähtömoduliin j vastaa kytkentää niiden välillä keskimodulin kautta.
Kun kokonaisluku f on riittävän suuri niin, että fCij ovat kokonaislukuja jokaisella i:llä ja j:llä. Ne muodostavat kapasiteettigraafin, jossa särmien lukumäärä solmujen i ja j välillä on vakio fCij. Koska kapasiteettigraafi on vakioasteinen (fm), sen polut voidaan määritellä fm:ään eri polkuun. On helppo todistaa, että jokainen fm-asteisen särmän polku kapasiteettigraafissa on superpositio f:n kuvaajan m-asteisen särmän polusta. Tietyn särmän polun määrääminen a Î {0,1,…,fm} kapasiteettigraafissa:
![]() (4)
(4)
jossa r Î {0,1,…,m-1} ja t Î {0,1,…,f-1} ovat f:llä jaettu osamäärä ja jakojäännös. Kuvaus g(a) = (t,r) joukosta {0,1,…,fm-1} à {0,1,…,f-1} x {0,1,…,m-1} on yksi-yhteen, esimerkiksi
![]()
eli polun määrääminen a tai vastaavasti (t,r) parin määrääminen särmien Ii ja Oj välillä vastaa kekimodulin r määräämistä reitiin Ii:stä Oj:hin t:nnessä aikavälissä joka syklissä. TDMA:ta vastaavasti jokaista sykliä kutsutaan kehykseksi ja periodia f kehyksen kooksi. Kuten kuvan 3 esimerkissä on kuvattu (m=3 ja kehyksen koko f=2), särmien polkujen hajaantuminen määrättyihin pareihin takaa, että reittimääritykset ovat joko tila- tai aikalimitettyjä. Siksi suhdetta (4) kutsutaan aika-tila -limitysperiaatteeksi.
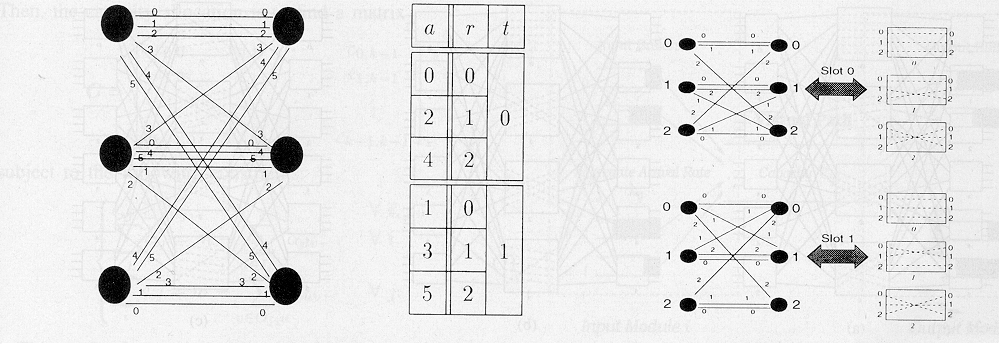
Kuva 3. Aika-tila -limitysperiaate.
Tasaisella liikenteellä, jossa liikenteen jakautuminen tulo- ja lähtömoduuleitten välillä on homogeeninen, jokaisen solmun fm särmää voidaan jakaa tasaisesti k:hon ryhmään, missäk on tulo(lähtö)modulien kokonaismäärä. Jokainen ryhmä sisältää g = (fm / k) särmää jokaisen I/O parin välillä, missä kehyksen koko f pitäisi valita sopivasti, jotta ryhmän koko g on kokonaisluku. Kapasiteetigraafin särmien polut voidaan valita "latinalaisen neliön" avulla, jossa jokainen Ai, 0 £ I £ k-1 vastaa joukkoa eri polkuja, esimerkiksi
![]()
Koska jokainen numero joukossa {0,1,…,fm-1} esiintyy vain kerran joka rivissä tai sarakkeessa taulukossa, se on laillinen särmäpolku kapasiteettigraafissa. Ii/Oj välisten särmien sijoitus a = (t,r) ilmaisee, että kekimoduli r kytkee tulomodulin I lähtömoduliin j t:nnessä aikavälissä joka kehyksessä. Esimerkiksi (m=3, k=2) voidaan valita f=2 ja siten g=3. Täten polkujen ryhmät ovat A0={0,1,2} ja A1={3,4,5}.
Koska edellisessä esimerkissä keskimodulien määrä m on suurempi kuin tulomodulien määrä k, on mahdollista, että useampi kuin yksi keskimoduli on kytektty johonkin I/O pariin aikavälissä. Jos m < k, keskimoduuleita ei ole riittävästi kaikille I/O pareille aikavälissä. Keskimodulien lukumäärä jokaista I/O paria kohden kehyksessä pitäisi olla sama tasaiselle tuloliikenteelle, jotta kapasiteettivaatimus täyttyy ja määrä vastaa g = fm / k. Tämä metodi on esitetty seuraavassa esimerkissä. Kun m = 4 ja k = 6, valitaan f = 3 ja g= 2. Keskimodulien lukumäärä I/O paria kohti on g = 2 jokaista f = 3 aikaväliä kohti.
III. Kapasiteetin ja polun määrittäminen
moninopeuksiselle liikenteelle
Yleisesti, liikenteen aiheuttama kuormitus eri I/O parien välillä ei ole tasaisesti jakautunutta. Tasainen kapasiteetin jakaminen aiheuttaisi virtuaalipoluille tarjotun kuorman epätasaista jakautumista, jonka seurauksena välitettäville paketeille aiheutuisi erisuuruia häviöitä ja viiveitä. Tästä johtuen, liikenteen ollessa epätasaista, rajallisen kapasiteetin varaaminen eri virtuaalipolulle tulisi riippua yhteyksien kuormasta.
Kapasiteetin määrittäminen
Kytkimen kapasiteetti voidaan jakaa kolmeen tasoon, kytkintasoon, yhteystasoon ja pakettitasoon. Kytkintason kapasiteetti voidaan käsittää kytkimen liikenteen kytkemiskapasiteettina. Se on määritelmänsä mukaan pakettien lukumäärä, jotka voidaan yhdessä aikavälissä reitittää sisääntulosta lähtöön. Se on kiinteä ja määräytyy keskimmäisen vaiheen modulien lukumäärän perusteella. Yhteystason kapasiteetti määräytyy kytkintason kapasiteetin perusteella. Yhteystasolla, kytkin varaa yhteydelle tietyn määrän kapasiteettia, ns. efektiivisen kaistaleveyden, jotta yhteyden vaatimat tilastolliset QoS parametrit täyttyvät (viive ja pakettien häviöt).
Merkitään a :lla (solua/aikaväli) sisääntulon u ja lähdön v välisen liikenteen vaatimaa efektiivistä kaistaleveyttä. Oletetaan, että yhteyden valvonta noudattaa seuraavia kapasiteetin varaussääntöjä:
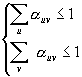
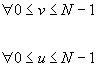 (5)
(5)
Kaikkien linkkien kapasiteettia ei välttämättä saada kokonaan hyödynnettyä, jolloin jäljelle jäänyt kaistaleveys voidaan antaa ARB-liikenteen käyttöön, joka on riipumaton viiveistä. ARB-palvelua voidaan tukea takaisinkytkentämekanismilla, jolla saadaan nopeasti tietoa verkon vapaana olevista resursseista. Oletetaan, että linkkien kapasiteettia rajoittaa seuraavat ehdot:
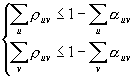
![]() (6)
(6)
Kuten kuvasta (4) selviää, on yhteenlaskettu ARB-liikenne sisääntulon I ja lähdön O välisellä virtuaalipolulla:
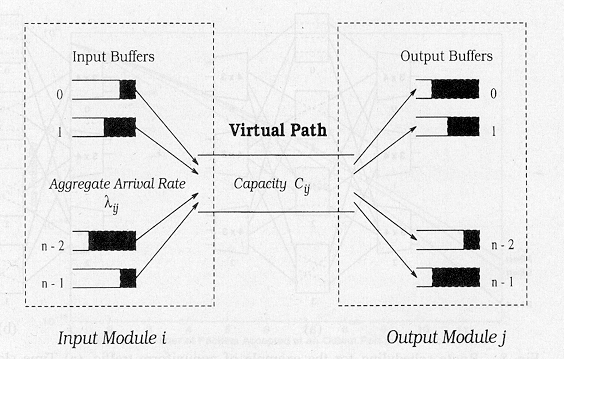
Kuva 4. Virtuaalipolku tulomoduli i:n ja lähtömoduli j:n välillä.
Oletetaan lisäksi, että keskimmäisen vaiheen k x k kytkin, joka kuvaa ARB liikennettä, on annettu:
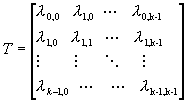 (7)
(7)
Tässä tapauksessa kapasiteetin varaus voidaan löytää matriisista:
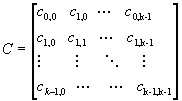
Kapasitteetin varauksen tarkoituksena on jakaa tarjolla oleva kaistanlaveys oikeudenmukaisesti ARB-solujen kesken. Tarjottu kuorma voidaan määritellä solujen keskimääräisenä saapumisnopeuteja jaettuna varatulla kaistanleveydellä. Ristikytkimessä voidaan minimoida seuraavaa kohdefunktiota:
![]() (8)
(8)
Vaihtoehtoisesti, jokaista virtuaalipolkua voidaan mallintaa riippumattomalla M/M/1 jonolla, jolle saapumistiheys on l ij ja palvelutiheys cij. Tällöin, pakettien keskimääräinen viive sisääntulosta lähtöön on:
![]() (9)
(9)
jolloin minimoitavaksi kohdefunktioksi saadaan:
![]() (10)
(10)
Sisääntulon Ii ja lähdön OI väliselle virtuaalipolulle varattu kapasiteetti on täten :
Reitin määrittäminen
Tarkastellaan ristikytkintä, jonka parametrit ovat n=3, k=3 ja n=4. Oletetaan lisäksi, että liikenne on ARB-tyyppistä. Mikäli liikennematriisi on seuraavanlainen:
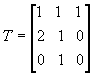 (11)
(11)
saadaan kapasiteetti laskettua kaavasta (12):
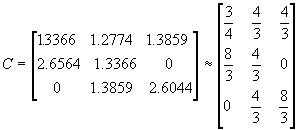 (12)
(12)
Yleensä, kapasiteettimatriisin termit eivät ole kokonaislukuja. Kuitenkin, kapasiteetin varaaminen f kokoiselle ikkunalle, f*C voidaan pyöristää kokonaisluvuiksi, jolloin pyöristysvirheet ovat kääntäen verrannollisia f:ään. Pyöristysvirhe voidaan siis tehdä äärettömän pieneksi kasvattamalla ikkunan kokoa. Ikkunan koon kasvattamista rajoittaa kuitenkin muistin koko, koska reititysinformaation määrä kasvaa suoraan verrannollisesti f:ään. Täten ikkunan koko on kompromissi pyöristysvirheiden ja muistin koon väliltä.Oletetaan seuraavassa, että kaikki eij=f*cij ovat kokonaislukuja, kun f on tarpeeksi suuri:
![]() (13)
(13)
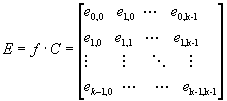 (14)
(14)
Yllä esitetyssä matriisissa, e esittää jokaisen I/O parin välisten janojen lukumäärää k x k kapasiteettikraafissa, jotka ovat astetta fm. Kuten aikaisemmin on mainittu, jokaisesta kraafista voidaan löytää fm polkua jossa jokainen polku esittää yhtä tiettyä aika-paikka väliä. Polun määrittämiseen voidaan käyttää ns. "complete matchin" tekniikkaa, jota sovelletaan rekursiivisesti solmujen kompleksisuuden vähentämiseksi. Tähän sopivia algoritmejaa ovat mm. Hungarian-algoritmi ja alternating-path-algoritmi.
IV Valitseminen ristikytkimen suorituskyvyn ja
monimutkaisuuden välillä
"Path Switching - A Quasi-Static Routing Scheme for Large-Scale ATM Packet Switches" dokumentin mukaan on pääasia ristikytkimen virtuaalipolun kytkinarkkitehtuurissa ja yhtenäisen verkonhallintamallin tarjoamisessa, lisäksi käsitelty suunnittelussa tarvittua tietoa kysymyksestä valinnassa solutason suorituskyvyn ja kytkimen monimutkaisuuden välillä.
Aluksi valitsemista on tutkittu erilaisen suorituskyvyn ja monimutkaisuuden välillä N x N Clos -verkossa parametreilla n, m ja k. Koska saapuva paketti kohdennetaan m x n lähtömoduliin, niin täytyy se vielä reitittää yhteen n lähtömoduliin, jolloin lähtömodulin monimutkaisuus kasvaa suhteessa n. Toisaalta suuri n -arvo merkitsee pientä k-arvoa N = nk kokoiselle kiinteälle kytkimelle ja liikennevirta kussakin virtuaalipolussa on tasaisempi johtaen parempaan staattisen multipleksauksen hyötyyn.
Oikeanlainen vertailu erilaisilla n ja (m / n) arvoilla täytyy perustua samaan määrään overheadia. Ristikytkimellä on kolmea tyyppiä overheadia: tulovälitys, tulomuisti ja lavennustekijä.
Ristikytkimen suorituskyvyssä ratkaiseva tekijä on (m / n) lavennustekijä. Eteenpäin valikoivan tulomodulin toteutuksessa haetaan paketteja peräkkäin ja paketti valitaan, jos sen kohdennettu lähtömoduli vastaa määritettyä reittiä reitityksessä. Haun laajuutta kutsutaan ikkunan kooksi ja mitä suurempi on ikkunan koko, sen parempi on läpäisy. Ikkunan koolla w ja modulin koolla n, maksimissan tutkittavien pakettien määrä on wn.
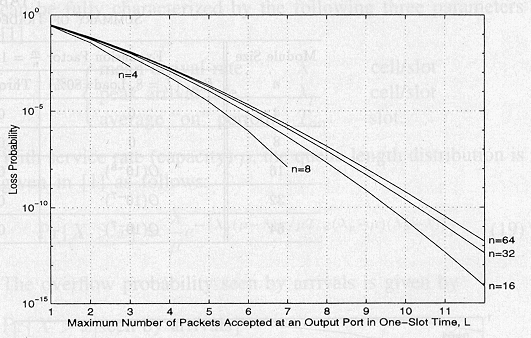
Analyysi osoittaa, kuinka paketin hävikkitodennäköisyys lähtömodulissa kasvaa vastaavasti lavennustekijän kanssa. Miten tahansa suuri lavennustekijä ei välttämättä tuota yhtään parempaa systeemin suorituskykyä. Kuvissa 5 ja 6 osoitetaan todeksi se, kuinka hävikkitodennäköisyys kasvaa vastaavasti parametrien n ja (m / n) kanssa.
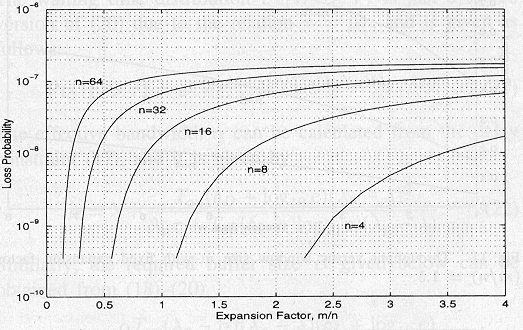
Kuva 5. Hävikkitodennäköisyys verrattuna L:ään 80 % Kuva 6. Hävikkitodennäköisyys verrattuna lavennusteki-
kuormalla. jään (m/n) kiinteän L=8 kanssa.
|
Moduli Koko n |
Lavennustekijä |
|
||
|
Ploss(L=8,Kuorma=80%) |
Läpäisys |
Ploss(L=8,Kuorma=80%) |
Läpäisys |
|
|
4 |
0 |
0,29 |
0 |
0,47 |
|
8 |
0 |
0,41 |
O(10-8) |
0,64 |
|
16 |
O(10-8) |
0,56 |
O(10-7) |
0,84 |
|
32 |
O(10-7) |
0,72 |
O(10-7) |
0,97 |
|
64 |
O(10-7) |
0,78 |
O(10-7) |
0,99 |
Taulukko I. Yhteenveto valinnoista modulikokona n.
Kuvien 7 - 10 perusteella on ilmeistä, että suuremmat n ja (m / n) arvot johtavat aina parempaan tulomodulin läpäisyyn eteenpäin valikoivan kaavan kanssa ensimmäisessä portaassa.
Kuvassa 7 verrataan läpäisyä ja erilaisia ikkunakokoja erilaisille moduleille kokoa n, kun vakioa on lavennustekijä (m / n). Kuvassa 8 läpäisy kasvaa vastaavasti lavennustekijän (m / n) kanssa. Kuitenkin suuret (m / n) ja w kasvattavat keskusportaan monimutkaisuutta ja vastaavasti prosessointiaikaa lähtöportaassa. Kuvassa 10 havaitaan, että suuremmat modulit toimivat paremmin.
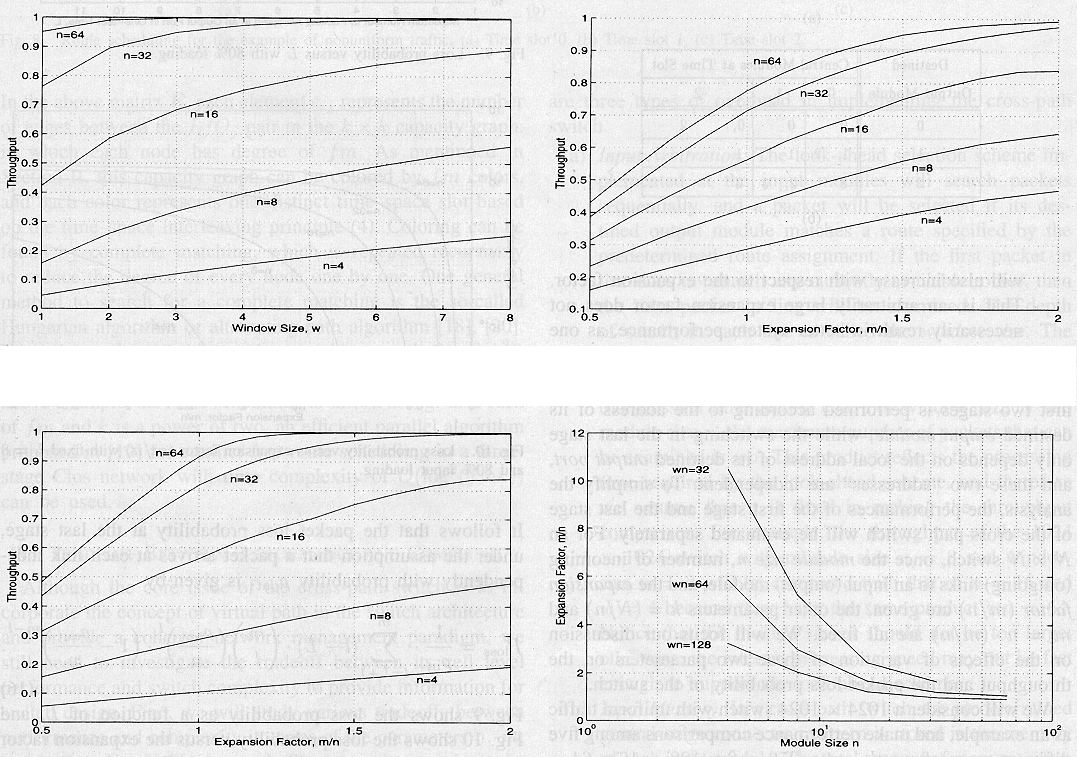
Kuva 7. (ylh. vas.) Läpäisy verrattuna ikkunakokoon w kiinteän lavennustekijän (m/n)=1.5 kanssa.
Kuva 8. (ylh. oik.) Läpäisy verrattuna lavennustekijään (m/n) kiinteän ikkunakoon w=4 kanssa.
Kuva 9. (alh. vas.) Läpäisi verrattuna lavennustekijään (m/n) kiinteän ikkunakoon ja modulikoon tulolla wn=64.
Kuva 10. (alh. oik.) Lavennustekijä (m/n) verrattuna modulikokoon n saavuttaen 80% läpäisyn usealle kiinteälle
ikkuna- ja modulikoon tulolle.
Taulukon 1. mukaan lähtömodulin hävikkitodennäköisyyden ja tulomodulin läpäisyn välillä valinta oikealle modulikoolle ja lavennustekijälle tulisi olla n = 16 ja (m / n) = 2, sekä vastaavasti kytkimen koolla N = 1024.
Tutkimuksen lopputulokset
"Path Switching - A Quasi-Static Routing Scheme for Large-Scale ATM Packet Switches" dokumentissa ehdotetaan kytkintä, joka on dynaamisen ja staattisen reititysyhdistelmän kompromissi.
Staattista piirikytkentää voitaisiin verrata rautatieverkkoon, missä rautatien radan alhainen hyötysuhde on seurausta radan vuoronjaosta ja junan varauksesta.
Kuitenkin dynaamisen reitityksen solukytkennän algoritmin laskennan monimutkaisuus rajoittaa kytkimen kehitystä.
Esitettyä ristikytkentää voitaisiin verrata myös liikennevalojen ohjaamaan autojen kulkuun risteyksessä, sillä se ei edellytä monimutkaista tai erityistä laitteistoa, mahdollistaen korkean hyötysuhteen.
Quasi-staattinen reititysyhdistelmä tarjoaa hajautetun kytkimen ohjauksen CLOS -verkossa, seurauksena sen yksinkertaisuudesta ja laajennettavuudesta.
Tämä esitetty kytkin käyttää toistaen ennaltamääritettyä keskusmodulin yhteyksien näytekuviota, siten että kukin yksittäinen moduli kykenee reitittämään paketteja pelkästään paikallisen informaation perusteella.
Tämän kytkimen suunnittelu sisältää joukon parametreja, jotka valitsemalla saavutetaan riittävän matala välityksen hävikkitodennäköisyys, kuten on esimerkiksi edellä kuvatussa 1024 * 1024 kytkimessä.
Puutteet ja parannusehdotus
Edellä kuvatussa tulovälityksen politiikassa tulomoduli ei ole huomioinut lähtöportissa olevaa kilpailua.
Suorituskykyä voidaan parantaa, jos samalle lähtöportille kussakin tulomodulissa kohdennettujen valikoitujen pakettien lukumäärää rajoitetaan yhdessä aikavälissä.
Tulevat tutkimukset
Lisäksi esitetään vielä tarpeelliseksi tutkia kytkimen laajentamista multicastingiin ja multimedialiikenteeseen vaihtelevin QoS vaatimuksin.