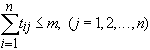 .
.
 cells simultaneously respective to each distinct switching plan of the
cells simultaneously respective to each distinct switching plan of the
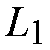 plans in a second switch, while each switch in each plane has capable of
delivering up to
plans in a second switch, while each switch in each plane has capable of
delivering up to
 cells simultaneously to an output port, where the
cells simultaneously to an output port, where the
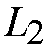 <
<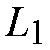 <<N
depends on the cell loss requirement and is independent of switching size. The
switch with a certain cell loss requirement can be ensured by choosing a
suitable path set of
<<N
depends on the cell loss requirement and is independent of switching size. The
switch with a certain cell loss requirement can be ensured by choosing a
suitable path set of
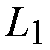 and
and
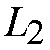 .
For instance, cell loss probability in the switch can be kept to less than 10[-6 ] for various N, under a 90% load, if a set of
.
For instance, cell loss probability in the switch can be kept to less than 10[-6 ] for various N, under a 90% load, if a set of
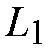 =9
and
=9
and
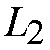 =4
(or
=4
(or
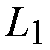 =8
and
=8
and
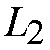 =5)
is chosen. This switch keeps a self-routing ability in which the cell routing
is based on a certain phase address. The small switching module achieves the
goal of relaxing the limitation of VLSI implementation. Currently, especially
for packet switching, the cost of the switch element has become less
significant; a greater proportion of the cost is for buffers' size in the case
of burst traffic. The output queue scheme reduces buffer number rather than
output buffers in both stages, thus it achieves the best delay/throughput
performance. Since each switching module is independent of others,
synchronisation is not required between modules.
=5)
is chosen. This switch keeps a self-routing ability in which the cell routing
is based on a certain phase address. The small switching module achieves the
goal of relaxing the limitation of VLSI implementation. Currently, especially
for packet switching, the cost of the switch element has become less
significant; a greater proportion of the cost is for buffers' size in the case
of burst traffic. The output queue scheme reduces buffer number rather than
output buffers in both stages, thus it achieves the best delay/throughput
performance. Since each switching module is independent of others,
synchronisation is not required between modules.Publication 2 discussed a detail about the MULTIPAR switch, including the growability and reliability of the switch. In the publication, we present three schemes to construct a large size switch from small size modules, and we show how a large switch size can be implemented by using the different growing schemes. Reliability is also an important issue for large switch. The MULTIPAR modular architecture limits the failure group size to a single module. The failure of a single module only disturbs local traffic. In the case of a failure of a single module, the worst case is a failure of the Batcher network in the first stage which disrupts the traffic of n input ports. Other failures, such as the banyan module in the first stage or the switching module in the second stage, only increase the cell loss rate and reduce the quality of communications.
Publication 3 discusses the impact of non-uniform traffic on the MULTIPAR switch. Since the general traffic pattern offers a complete coverage for any imbalance pattern, but has difficulty provid by a systematic study of the system, i.e., there are too many parameters, we use a bi-group imbalance traffic pattern. In practice, this means that some sources communicate with some destinations (favorite groups) more frequently compared to other destinations. Publication 3 respectively gives the definitions of output imbalance, input imbalance, as well as input and output imbalance traffic, moreover it gives the equations of packet loss probability in the two-stage MULTIPAR switch. In publication 3, we investigate the impact on cell loss probability in the concentrator due to the non-uniform traffic, and estimate the number of concentrator outputs needed. Our results prove that the output imbalance traffic has heavier packet loss than the input imbalance traffic or both simultaneous input and output imbalance, according to our definition.
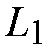 simultaneous cells in any first stage switch arriving to a given second stage
switch is extremely small, while the probability of more than
simultaneous cells in any first stage switch arriving to a given second stage
switch is extremely small, while the probability of more than
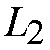 simultaneous cells in any second stage switch arriving to a given output port
of a second stage switch is also extremely small. Every switching module in
each stage is a nonblocking output queue switch which is constructed by a
simplified Sunshine switch. The simplified Sunshine
switch enables delivery of up to
simultaneous cells in any second stage switch arriving to a given output port
of a second stage switch is also extremely small. Every switching module in
each stage is a nonblocking output queue switch which is constructed by a
simplified Sunshine switch. The simplified Sunshine
switch enables delivery of up to
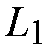 (or
(or
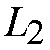 )
cells destined for a same second stage module (or destination) to the same
output port simultaneously. The publication also describes how to construct the
simplified Sunshine switch composed of a Batcher network and a group of
parallel banyan networks. For independent random load conditions, the
BNS has less than
)
cells destined for a same second stage module (or destination) to the same
output port simultaneously. The publication also describes how to construct the
simplified Sunshine switch composed of a Batcher network and a group of
parallel banyan networks. For independent random load conditions, the
BNS has less than
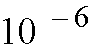 cell loss probability with eight concentrator outputs in every stage switching
module, i.e.,
cell loss probability with eight concentrator outputs in every stage switching
module, i.e.,
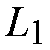 =
=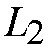 =8.
This structure takes full advantage of small switching hardware complexity and
self-routing capability, especially in the case of uniform random traffic. The
switch size can be enormously increased by increasing the dimension of each
switch module. However the switch architecture requires large buffer size,
especially in the case of bursty traffic.
=8.
This structure takes full advantage of small switching hardware complexity and
self-routing capability, especially in the case of uniform random traffic. The
switch size can be enormously increased by increasing the dimension of each
switch module. However the switch architecture requires large buffer size,
especially in the case of bursty traffic.
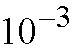 and date transmission service can bear a cell loss probability of
and date transmission service can bear a cell loss probability of
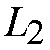 [CCI90]. Introducing priorities to different classes of cells is one way to the
maintain quality of services and reduce switching hardware complexity. Several
previous works have investigated the performance of a no-priority
Knockout switch under uniform, non-uniform and bursty traffic [Yen87,
Eng89, Yoo88, Eng91]. The performance of output queuing switches depends
primarily upon the number of simultaneous cells accepted and the number of
buffers. Several papers have studied the various priority queuing schemes of
the switches [Che91b, Che92, Krö91]. In publication 6, we mainly focus on
analyzing the cell loss within the priority Knockout Switch and
the priority Generalized Knockout Switch due to the number of
simultaneous cells accepted, L, for the two-class priority scheme. By
utilizing the priority schemes in the Knockout Switch and the
Generalized Knockout Switch, the priority switches achieve extremely
small cell loss for high-priority cells, far beyond that for the no-priority
Knockout Switch and the Generalized Knockout Switch, with little
impact on low-priority cells. In addition the priority schemes are more
efficient in the Generalized Knockout Switch than in the Knockout
Switch to reduce the interconnect complexity of the switch.
[CCI90]. Introducing priorities to different classes of cells is one way to the
maintain quality of services and reduce switching hardware complexity. Several
previous works have investigated the performance of a no-priority
Knockout switch under uniform, non-uniform and bursty traffic [Yen87,
Eng89, Yoo88, Eng91]. The performance of output queuing switches depends
primarily upon the number of simultaneous cells accepted and the number of
buffers. Several papers have studied the various priority queuing schemes of
the switches [Che91b, Che92, Krö91]. In publication 6, we mainly focus on
analyzing the cell loss within the priority Knockout Switch and
the priority Generalized Knockout Switch due to the number of
simultaneous cells accepted, L, for the two-class priority scheme. By
utilizing the priority schemes in the Knockout Switch and the
Generalized Knockout Switch, the priority switches achieve extremely
small cell loss for high-priority cells, far beyond that for the no-priority
Knockout Switch and the Generalized Knockout Switch, with little
impact on low-priority cells. In addition the priority schemes are more
efficient in the Generalized Knockout Switch than in the Knockout
Switch to reduce the interconnect complexity of the switch.
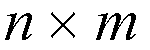 )
inputs and outputs, in the first and the third stage there are n
)
inputs and outputs, in the first and the third stage there are n
 switches, while in the middle stage there are m
switches, while in the middle stage there are m
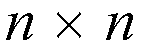 switches. The first two stage's switches the crossbar ones are controlled by a
central controller. We discuss how to map the path rearrangement problem in the
three-stage Clos' packet switch to a mathematical problem that is to
find a set of permutation matrix from a packet traffic matrix. We define the
switches. The first two stage's switches the crossbar ones are controlled by a
central controller. We discuss how to map the path rearrangement problem in the
three-stage Clos' packet switch to a mathematical problem that is to
find a set of permutation matrix from a packet traffic matrix. We define the
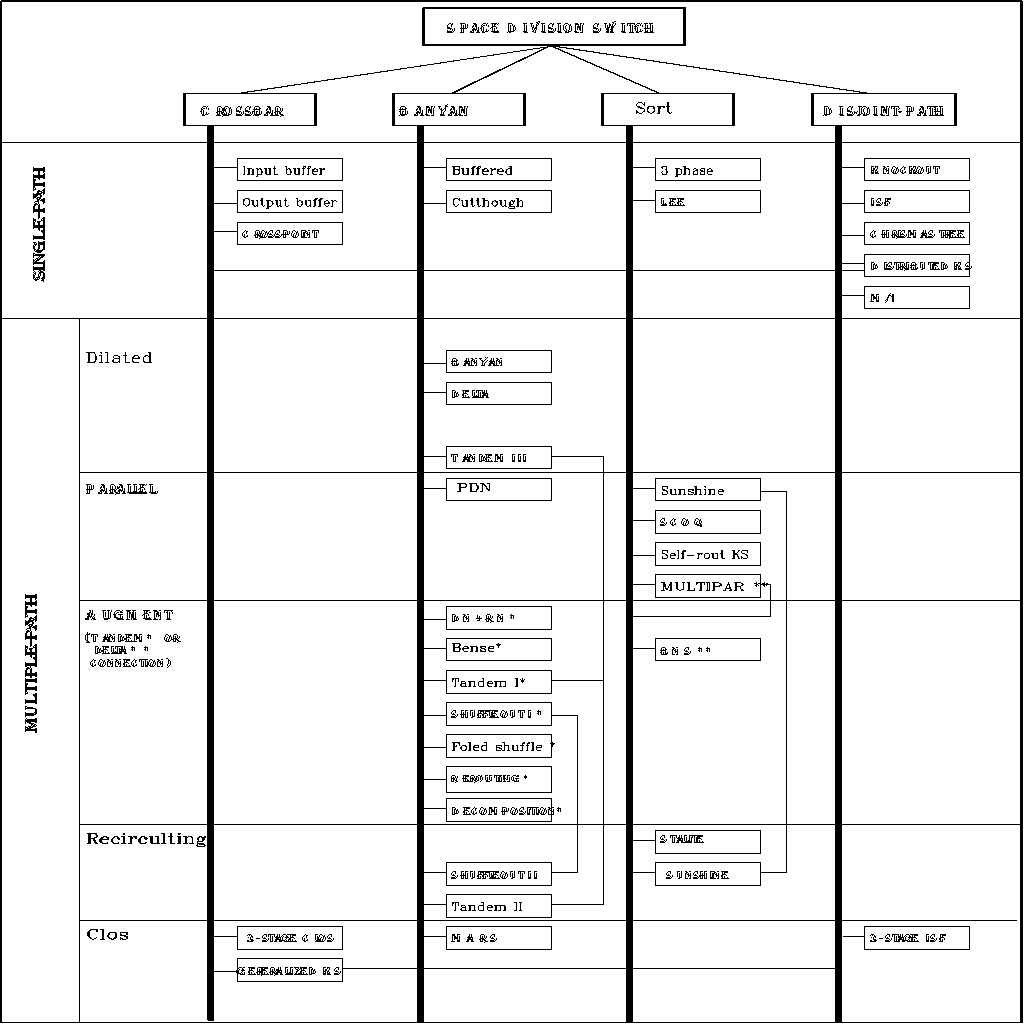
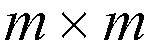 traffic matrix T, where the matrix element
traffic matrix T, where the matrix element
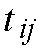 represents the number of packets arriving at the i-th first stage switch
and destined for the j-th third stage switch, and
represents the number of packets arriving at the i-th first stage switch
and destined for the j-th third stage switch, and
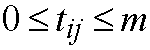 .
Since in the input of the switch we assume that arbitration logic is used to
solve the output contention, so the sum of the elements in each column and row
respectively are
.
Since in the input of the switch we assume that arbitration logic is used to
solve the output contention, so the sum of the elements in each column and row
respectively are
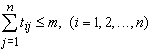
and
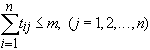 .
.
The path arrangement is to assign the T matrix into m
permutation matrices as
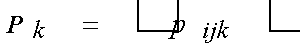 ,
,
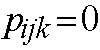 or 1, (k=1, 2, ..., m; i, j=1, 2, ..., n, ) where the sums of
the elements in each row and each column do not exceed 1. In publication 7, we
introduce two approaches: "step-by-step" approach and "global" approach.
or 1, (k=1, 2, ..., m; i, j=1, 2, ..., n, ) where the sums of
the elements in each row and each column do not exceed 1. In publication 7, we
introduce two approaches: "step-by-step" approach and "global" approach.
Step-by-step approach: The step-by-step scheme also proposed in papers
[Ma91, 92] is based on the formulas:
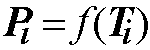 ,
,
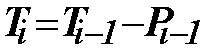 and
and
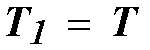 .
The f() is an assigning neural network algorithm; it is a Hopfeild model
which has already been used in the crossbar switch [Ali89, Tro91]. Therefore,
the approach needs m times the neural network convergence period, but,
the neural network has few numbers of neurons of O(
.
The f() is an assigning neural network algorithm; it is a Hopfeild model
which has already been used in the crossbar switch [Ali89, Tro91]. Therefore,
the approach needs m times the neural network convergence period, but,
the neural network has few numbers of neurons of O(
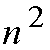 )
and interconnections of O(
)
and interconnections of O(
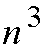 ).
).
Global approach: To reduce the convergence period, we propose the global
approach. The neural network is constructed in a 3-dimension space. Each plane
of the neural network is associated with a switch of the middle stage. A very
important contribution in the publication is finding out the dynamics' equation
of each neuron. The equation indicates the state of each neuron which is
changed simultaneously. The computation of the optimizing path arrangement only
needs one convergence period of the neural network. However, the neural network
has O(
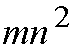 )
neurons and O(
)
neurons and O(
 )
interconnections.
)
interconnections.
In publication 7, we report simulation results based on an
N[[??]]N (N=16, n=m=
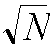 )
Clos' packet switch. The step-by-step approach can rapidly assign an
optimal path arrangement after
)
Clos' packet switch. The step-by-step approach can rapidly assign an
optimal path arrangement after
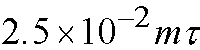 where [tau] is a time constant of each neuron, while the global approach scheme
needs only
where [tau] is a time constant of each neuron, while the global approach scheme
needs only
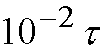 convergence time which is about m times faster than the step-by-step
scheme and is independent of number of input/output lines.
convergence time which is about m times faster than the step-by-step
scheme and is independent of number of input/output lines.
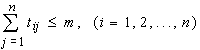
and
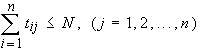 .
.
The path assignment algorithm is to find these permutation matrices of
 with
with
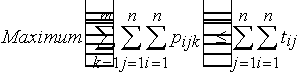 .
In publications 8 and 9, we use the same 3-dimension approach of neural network
as in publication 7.
.
In publications 8 and 9, we use the same 3-dimension approach of neural network
as in publication 7.
In publication 9, we scan a band of several weight values of the neural network for the choice of the appropriate weight parameter set by the computer simulations. The appropriate parameter set has been found for the neural network application. The simulation results have shown that the neural network path establishment algorithm can find the sub-optimal throughput, the efficiency of which is 99% after 200 iterations of the neural networks. A significant advantage of the neural network approach has been proved in the simulations which show that the neural network convergent time is independent of switch size.
The author's contribution to the publication 1 to 9 has been essential. He has developed the theoretical framework, and performed most of the simulations. The main contribution in the thesis is as follows. Publication 1 is the author's own work. He has developed a novel ATM switch architecture, and has given the theoretical analysis method of the switch performance. In publication 2, the author has developed the switch, and given a detailed analysis and simulations. In publication 3, the author has studied the impact of non-uniform traffic, gave the definition of three uniform traffic models and equations of cell loss probability. In publication 4, the author has proposed another ATM switch architecture and studied the performance of the switch. In publication 5, the author's contribution is to do simulations of cell loss in the two switches and to compare them. In publication 6, the author theoretically analyzes the priority effect on the output queuing switch (i.e., Knockout switch and Generalized Knockout switch), derive cell loss probabilities for the two class priority cells, and give important results. In publications 7, 8 and 9, the author discovered a neural network equation which can be used in the path establishment of the rearrangeable Clos' switch which has been proved to have fast convergence time. The author has performed the main work such as theoretical analysis and simulations, in publication 7. In publications 8 and 9, the author has proposed using the neural network algorithm in an input and output queuing Clos' packet switch as a path arrangement algorithm, derived most of the formulas of the neural network, and guided the co-author in the simulations.