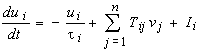
Optimization problems are typically implemented on a feedback network. These
networks interconnect the neurons with a feedback path. A typical feedback
neural network is the Hopfield neural network [Hop85]. Figure 4 shows the
circuit structure of the neuron and its functional structure. This differential
equation describes the neuron:
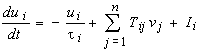
(1)
where
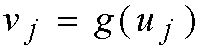(j=1,2..., n), and g( ) is the sigmoid activation function. It is shown in
[Hop85] how to choose the values of synapse
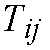so that (1) represents the dynamics corresponding to a given energy function.
If the energy function corresponds to an optimization objective, the
initialization of the
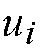's
to an initial configuration will result in an equilibration which settles to a
local minimum of the objective function. One famous example using the neural
networks is the Traveling Salesman Problem (TSP) [Wil88], in which a salesman
is supposed to tour a number of cities (visiting each exactly once, then
returning to where he started) and desires to minimize the total distance of
the tour. The intercity distances are given as the input, and the desired
output is the shortest (or near-shortest tour). The operation of the feedback
network implies a descent on energy surface. In order to implement a solution
to the TSP, or any other optimization problem on a feedback network, the energy
function is used as a medium. By designing the network so that the minimum of
the energy function coincides with a minimum-length tour, the network becomes a
computer that searches for the minimum tour. This example stirred great
excitement since it suggested that the TSP could be solved approximately,
using an analog circuit in microseconds.
The highly interconnected architecture of switching networks suggests
similarities to neural networks. The papers [Tro91, Mar89, Ali88] considered
how to schedule packet transmissions through a complete
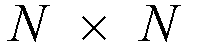crossbar switch. They constructed an
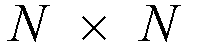traffic matrix. The optimization problem is to select a set of 1's in the
traffic matrix to form a permutation matrix, whose overlap with the traffic
matrix is maximized - this minimizes the blocking for that time slot. The
neural network is constructed with one neuron for each switch crosspoint, the
network is initialized with the traffic values and the network is allowed to
settle to form the permutation matrix.
A more complex approach by using the neural network is to assign an optimal
path arrangement in a three-stage Clos' packet switch. The optimization problem
is not only to select one permutation matrix in a traffic matrix, but several
permutation matrices, the sum of whose overlap is maximized. This approach has
been proposed in publications 7, 8 and 9.
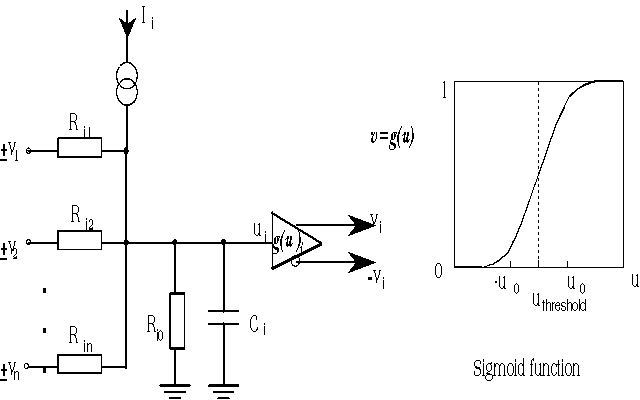
Figure 4 Hopfield model of a dynamic basic neuron cell.